MPA tool tries to align the peaks from multiple
chromatographic profiles. Profiles may have different curve shapes reflecting a differential protein expression making automatic comparison a hard task. In these cases the manual intervention is the only way to get the right alignment. Methods based on automatic approaches (i.e Correlation, Fast Fourier Transform, etc.) usually fail and are not able to recognize common features among profiles. Here we propose a novel strategy that is totally independent from the overall shape of the chromatographic profiles since it is based only on the peak position by making use of retention times (RT).
The original idea derives from the algorithm used in progressive
multiple sequence alignment (MSA). The MPA tool has been designed following a similar approach. Rather than treating with either DNA or protein sequences the algorithm has been adapted to align numerical data using a modified version of global alignment dynamic programming and refined progressive profile alignment.
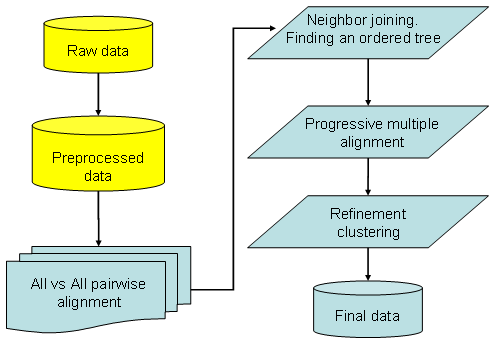
The overall strategy is divided in different steps:

|
2 | |
| 3 | ||
| 1 | 4 |
1) ALL VS ALL Pairwise alignment
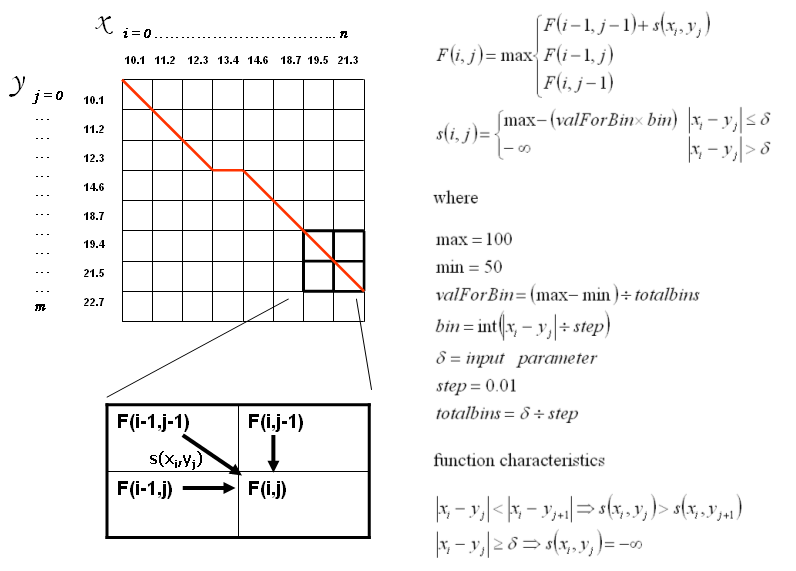
The algorithm is based on dynamic programming for solving problems exhibiting the properties of overlapping subproblems and optimal substructure. The idea is based on a 'ad hoc' modified version of the Needleman Wunch algoritm (JMB 1970) for global alignment. The goal is to find the optimal path in a matrix where peaks of chromatographic profile X should align to peaks of chromatographic profile Y (see figure below). The alignment is performed using the numerical values of the retention times save they satisfy the allowed time distance defined by the parameter δ. The conditions defined for s(Xi,Yj) are:
NJ finds the right order to add chromatographic profiles to the growing multiple alignment using the neighbor joining tree algorithm (Saitou and Nei, Mol Biol Evol 1987). The algorithm builds a matrix of distances and progressively finds the best order to align the chromatographic profiles. It is originally used in phylogenetic analysis and Multiple Sequence Alignments algorithms (such as Clustalw - Thompson et al. NAR 1994). It provides a single-tree topology, after a cascade of greedy pairing decisions, that reflects the order to follow for building the multiple alignment. NJ starts clustering the profiles from the highest scoring pair calculated in the first step of the "all vs all pairwise alignment".
3) Progressive multiple alignment
Progressive alignment is used to add one chromatographic profile at a time using dynamic programming as described, in principle, in point 1). The algorithm follows the order of the previously calculated NJ tree.
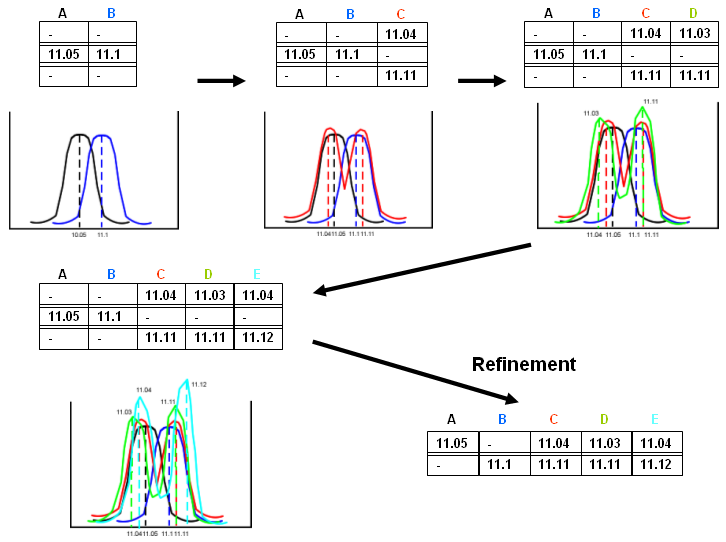
Refinement adjusts possible errors (once a gap always a gap in progressive euristic strategy). A typical error is simulated in the figure below showing that in the growing multiple alignment some errors may occur and are fixed. In the example the profiles have no RT shifts and δ <= 0.05. profile A and B satisfy the constraint and are aligned. Profiles C, D, E, added following strategy in point 3), reveal that peaks should not be clustered together since they belong to differently separated proteins. Refinement step is a post-processing check able to solve most of these discrepancies.